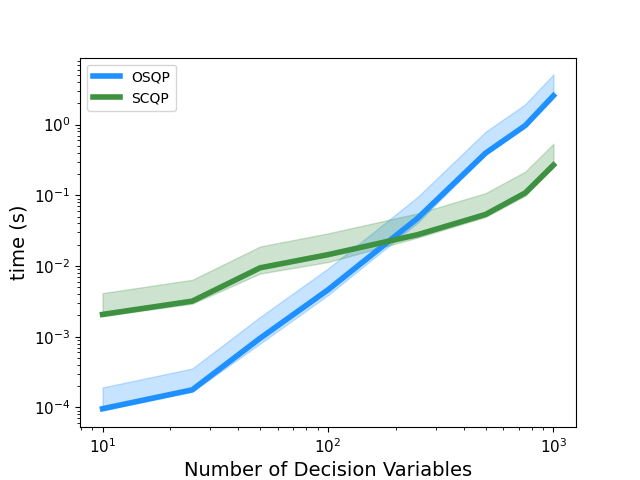
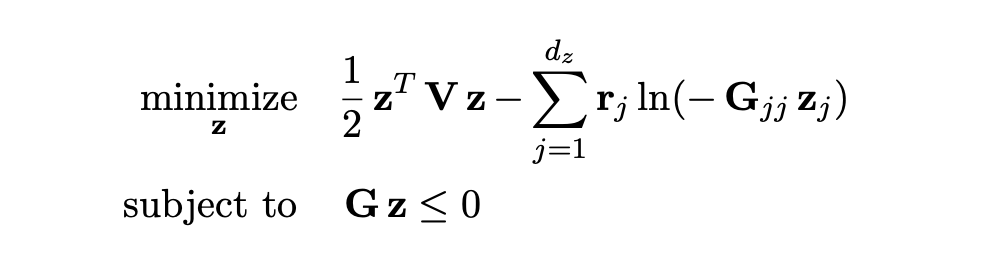Projects and Publications
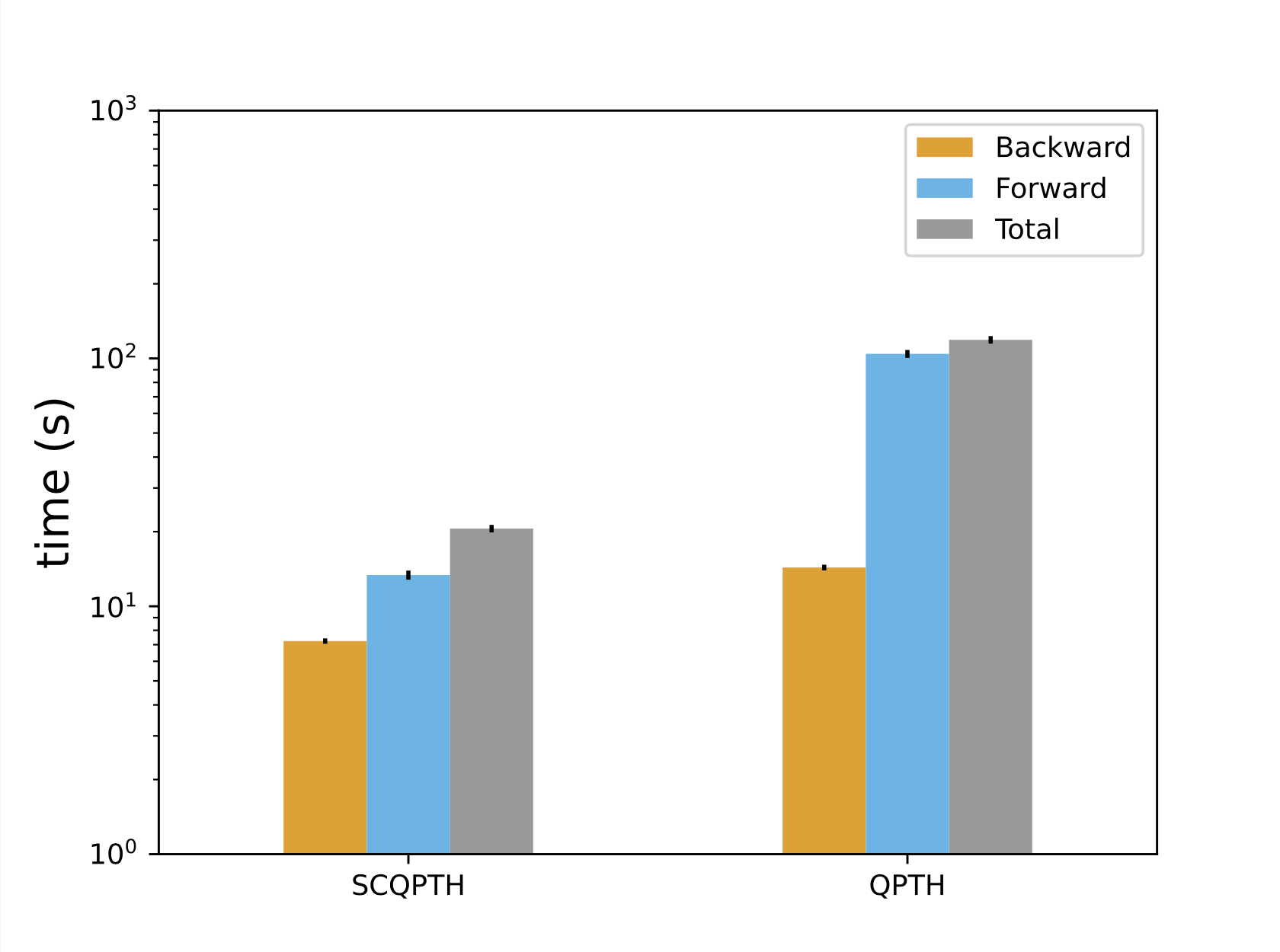
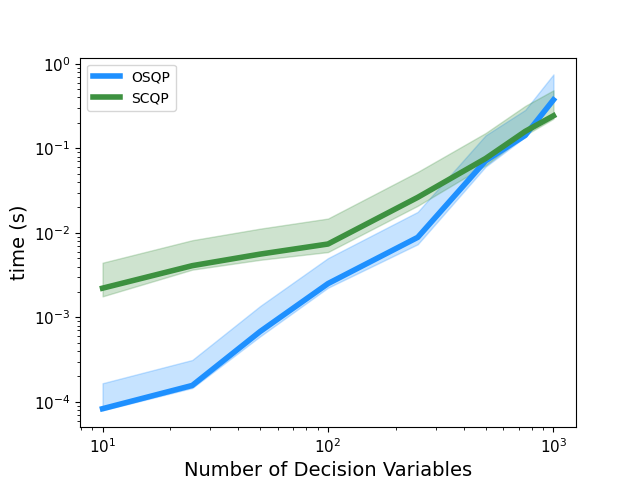
SCQPTH: differentiable splitting method for convex QPs
| Runtime: n = 100, m = 200 | Convergence |
|---|
 |  |
Paper
A Butler. SCQPTH: an efficient differentiable splitting method for convex quadratic programming. Abstract
We present SCQPTH: a differentiable first-order splitting method for convex quadratic programs. The SCQPTH framework is based on the alternating direction method of multipliers (ADMM) and the software implementation is motivated by the state-of-the art solver OSQP: an operating splitting solver for convex quadratic programs (QPs). The SCQPTH software is made available as an open-source python package and contains many similar features including efficient reuse of matrix factorizations, infeasibility detection, automatic scaling and parameter selection. The forward pass algorithm performs operator splitting in the dimension of the original problem space and is therefore suitable for large scale QPs with 100 to 1000 decision variables and thousands of constraints. Backpropagation is performed by implicit differentiation of the ADMM fixed-point mapping. Experiments demonstrate that for large scale QPs, SCQPTH can provide a 1x - 10x improvement in computational efficiency in comparison to existing differentiable QP solvers. Preprint Code
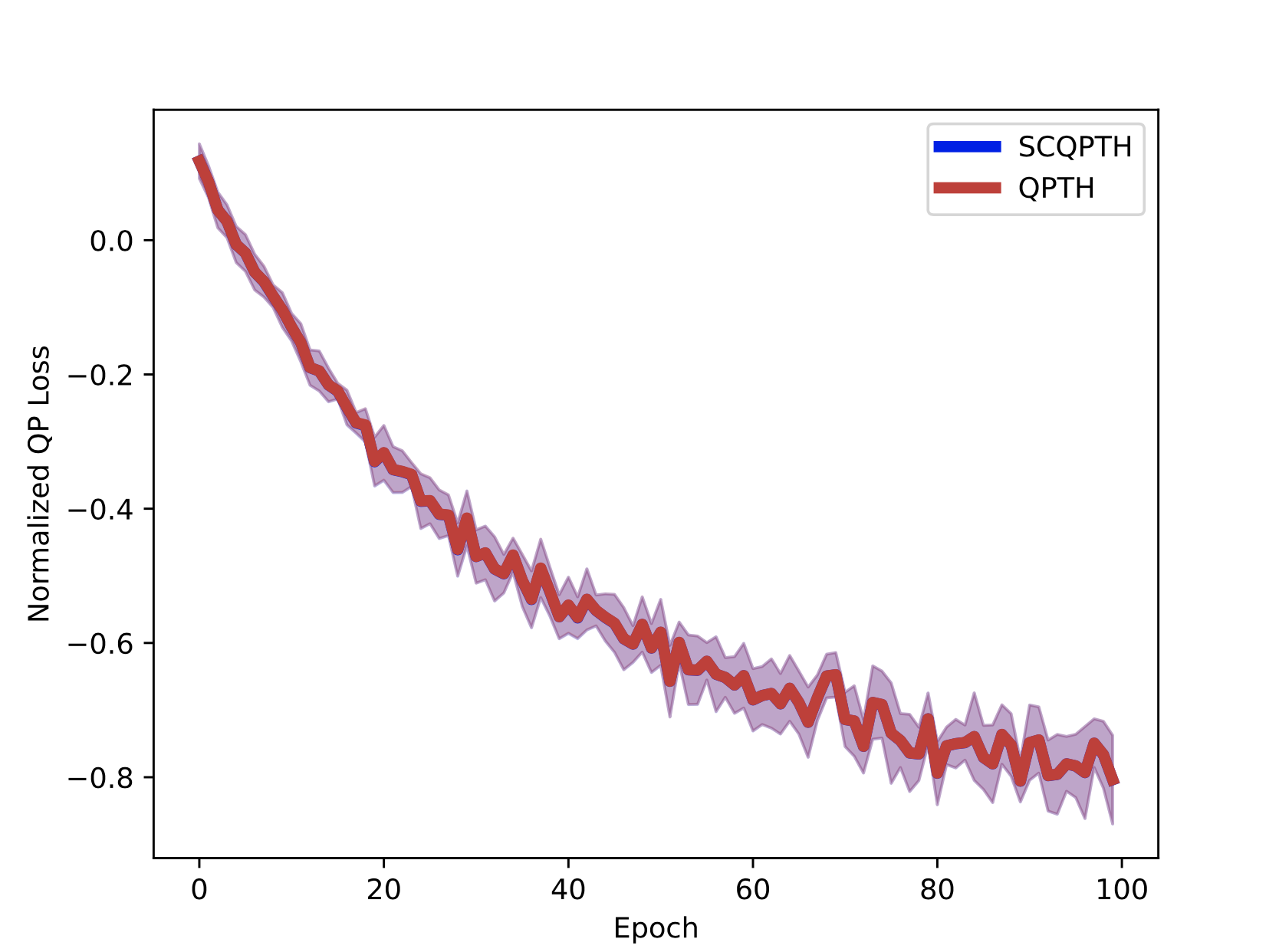
SCQP: A dense ADMM QP solver
| Dense QP: m = n | Sparse QP: m = n |
|---|
 |  |
Description
SCQP is a first-order splitting method for convex quadratic programming. The QP solver is implemented in numpy (for dense QPs) and scipy (for sparse QPs) and invokes a basic implementation of the ADMM algorithm. Code
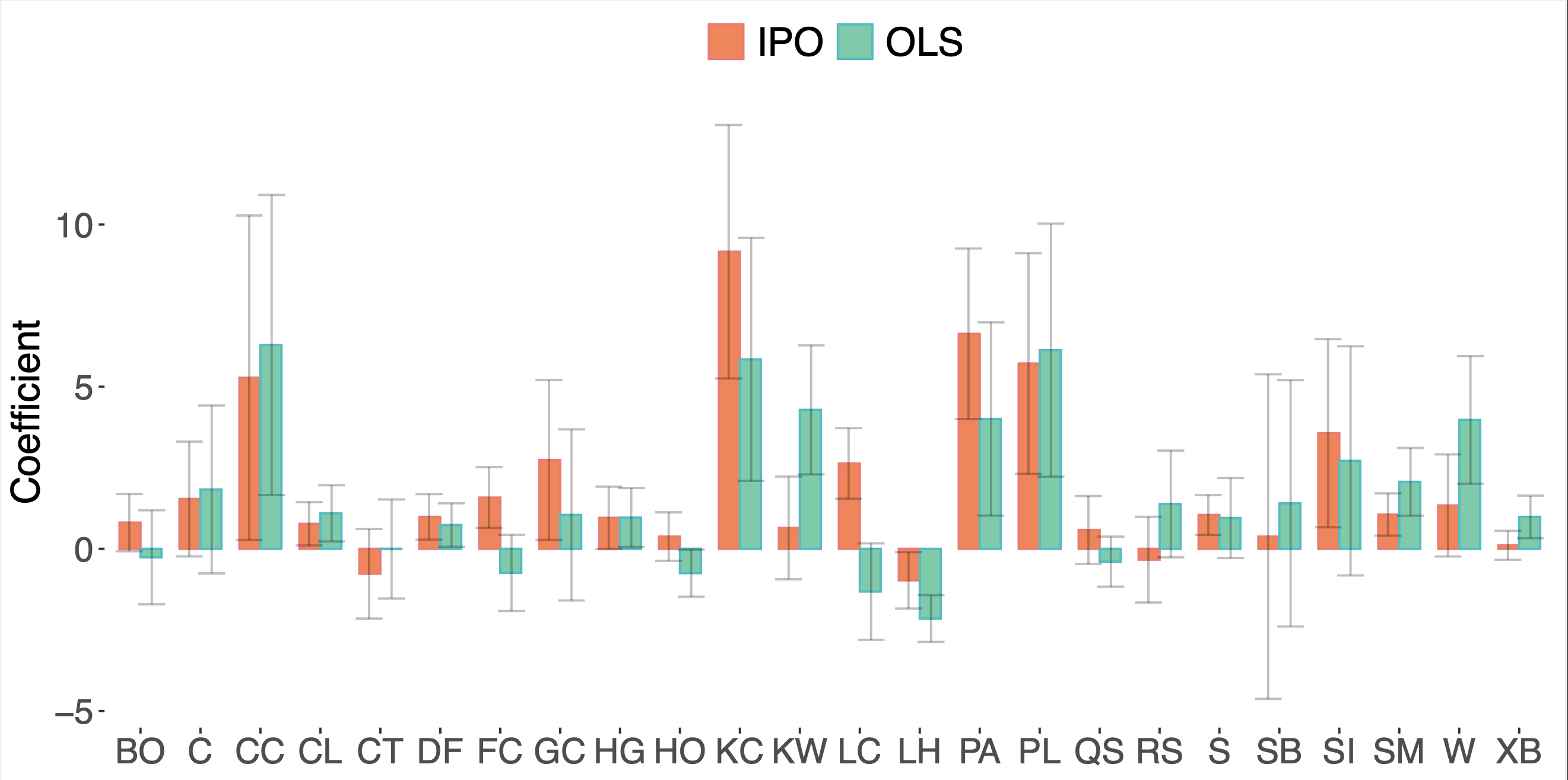
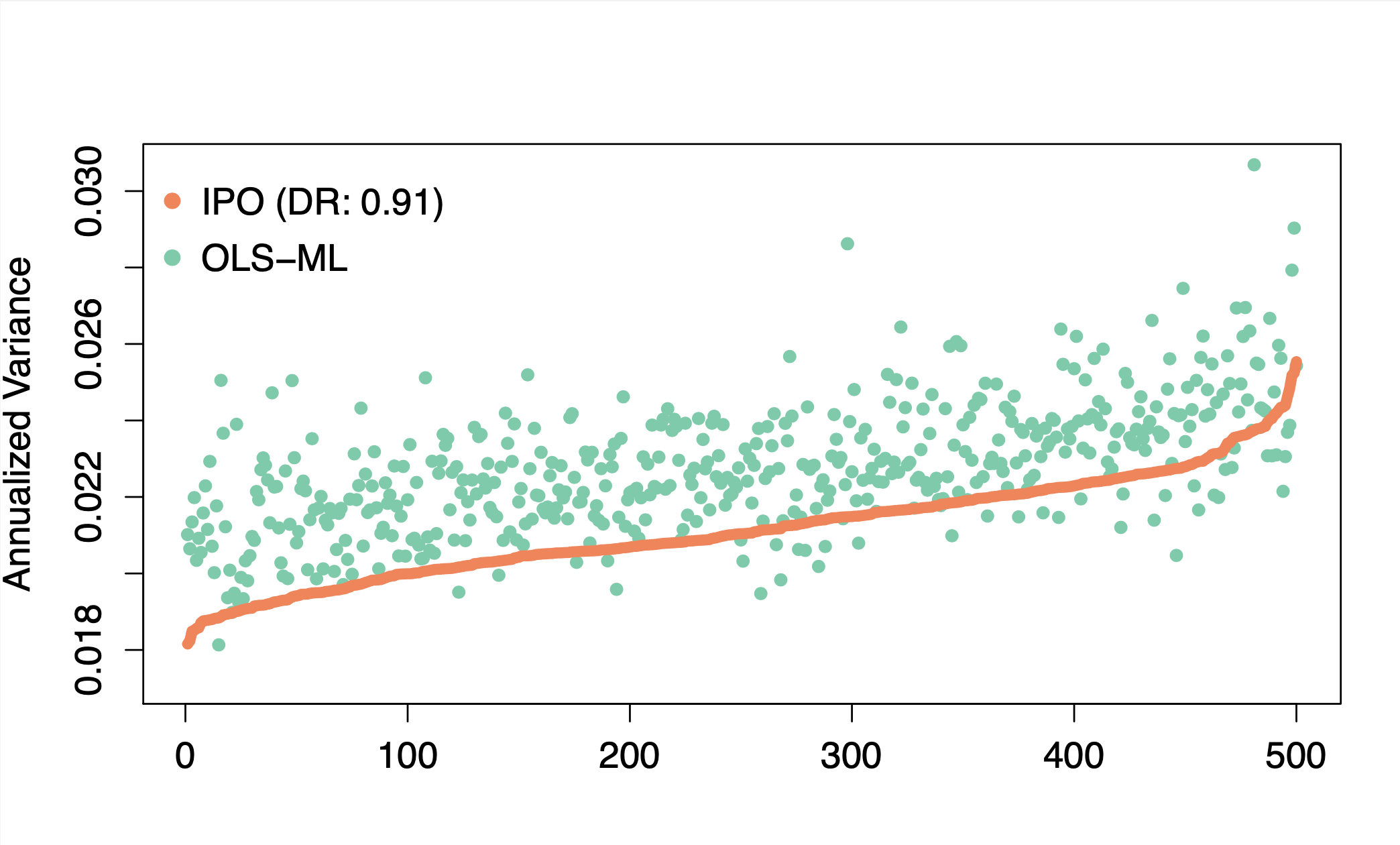
Integrating prediction in mean-variance portfolio optimization
Paper
A Butler, RH Kwon. Integrating prediction in mean-variance portfolio optimization. Quantitative Finance. 2023. Abstract
Prediction models are traditionally optimized independently from their use in the asset allocation decision-making process. We address this shortcoming and present a framework for integrating regression prediction models in a mean-variance optimization (MVO) setting. Closed-form analytical solutions are provided for the unconstrained and equality constrained MVO case. For the general inequality constrained case, we make use of recent advances in neural-network architecture for efficient optimization of batch quadratic-programs. To our knowledge, this is the first rigorous study of integrating prediction in a mean-variance portfolio optimization setting. We present several historical simulations using both synthetic and global futures data to demonstrate the benefits of the integrated approach. Paper Preprint
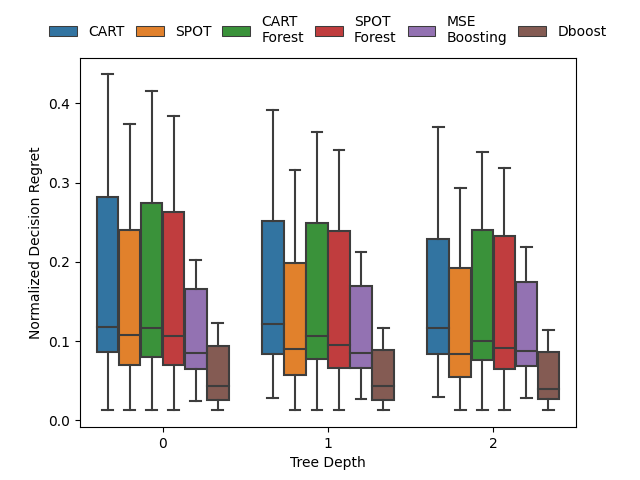
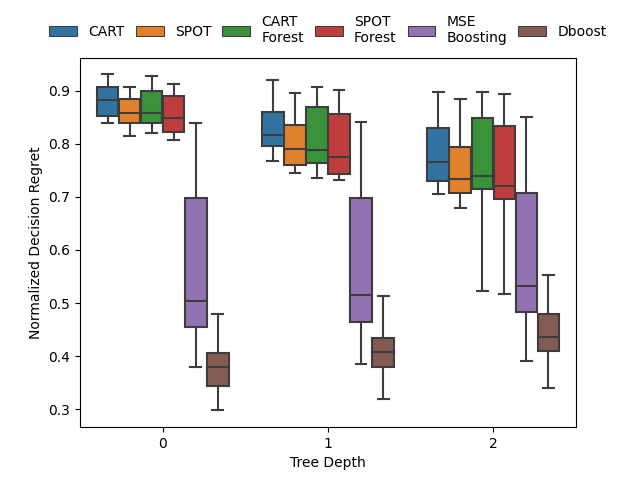
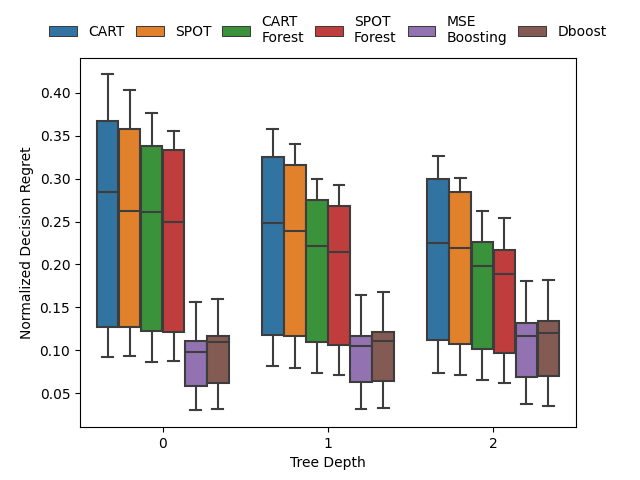
Gradient boosting for convex cone predict and optimize problems
| Network Flow Problem | Noisy Quadratic Program | Portfolio Optimization |
|---|
 |  |  |
Paper
A Butler, RH Kwon. Gradient boosting for convex cone predict and optimize problems. Operations Research Letters. 2023. Abstract
Prediction models are typically optimized independently from decision optimization. A smart predict then optimize (SPO) framework optimizes prediction models to minimize downstream decision regret. In this paper we present dboost, the first general purpose implementation of smart gradient boosting for predict, then optimize problems. The framework supports convex quadratic cone programming and gradient boosting is performed by implicit differentiation of a custom fixed-point mapping. Experiments comparing with state-of-the-art SPO methods show that dboost can further reduce out-of-sample decision regret. Paper Preprint Code
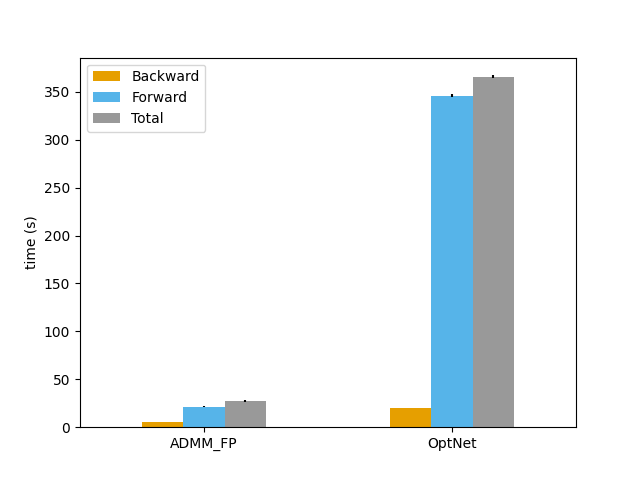
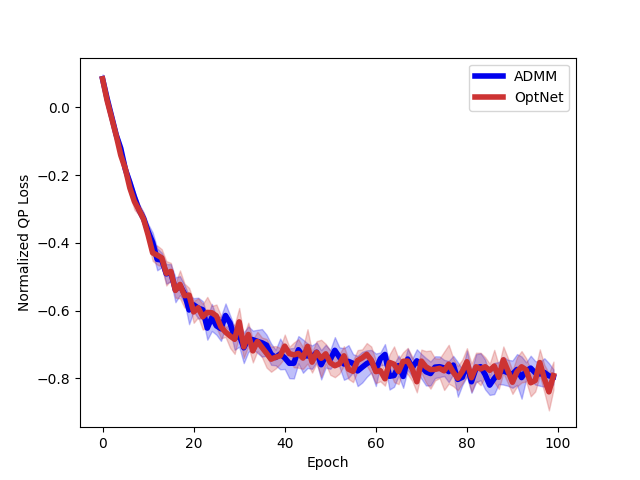
Efficient differentiable quadratic programming layers
| Runtime: dz = 500 | Convergence: dz = 500 |
|---|
 |  |
Paper
A Butler, RH Kwon. Efficient differentiable quadratic programming layers: an ADMM approach. Computational Optimization and Applications. 2022. Abstract
Recent advances in neural-network architecture allow for seamless integration of convex optimization problems as differentiable layers in an end-to-end trainable neural network. Integrating medium and large scale quadratic programs into a deep neural network architecture, however, is challenging as solving quadratic programs exactly by interior-point methods has worst-case cubic complexity in the number of variables. In this paper, we present an alternative network layer architecture based on the alternating direction method of multipliers (ADMM) that is capable of scaling to moderate sized problems with 100–1000 decision variables and thousands of training examples. Backward differentiation is performed by implicit differentiation of a customized fixed-point iteration. Simulated results demonstrate the computational advantage of the ADMM layer, which for medium scale problems is approximately an order of magnitude faster than the state-of-the-art layers. Furthermore, our novel backward-pass routine is computationally efficient in comparison to the standard approach based on unrolled differentiation or implicit differentiation of the KKT optimality conditions. We conclude with examples from portfolio optimization in the integrated prediction and optimization paradigm. Paper Preprint Code
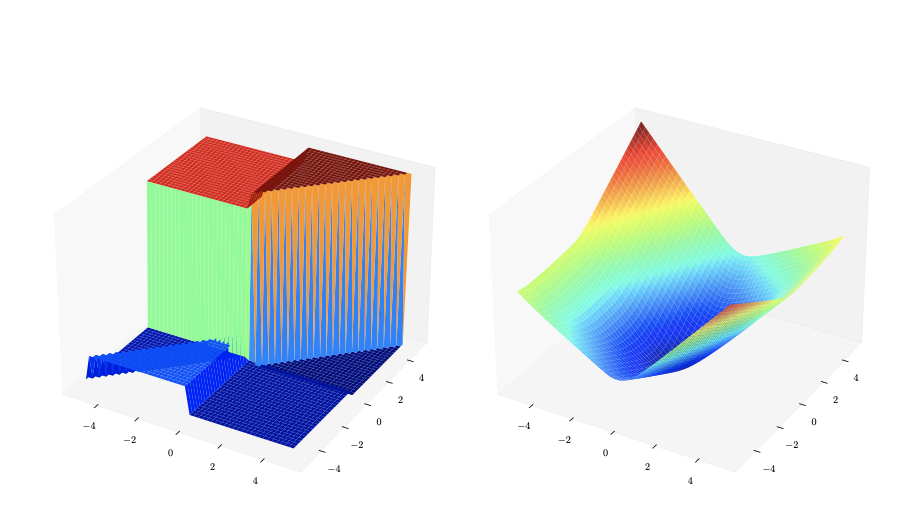
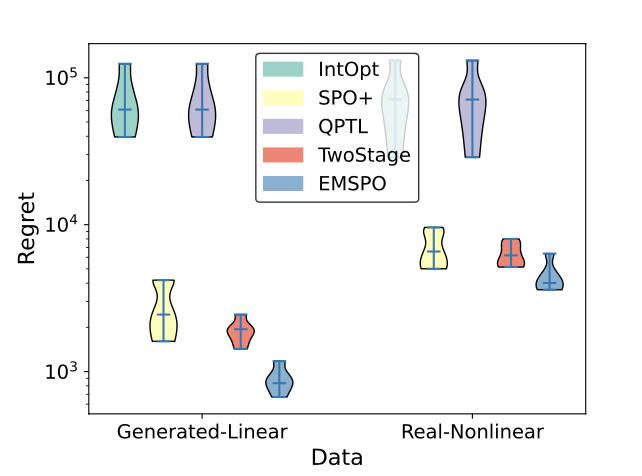
Exact symbolic solver for linear SPO
| SPO loss surface | Decision regret |
|---|
 |  |
Paper
J Jeong, P Jaggi, A Butler, S Sanner. An Exact Symbolic Approach for Benchmarking Predict-then-Optimize Solvers. In Proceedings of the 39th International Conference on Machine Learning (ICML-22). Abstract
Predictive models are traditionally optimized independently of their use in downstream decision-based optimization. The ‘smart, predict then optimize’ (SPO) framework addresses this shortcoming by optimizing predictive models in order to minimize the final downstream decision loss. To date, several local first-order methods and convex approximations have been proposed. These methods have proven to be effective in practice, however, it remains generally unclear as to how close these local solutions are to global optimality. In this paper, we cast the SPO problem as a bi-level program and apply Symbolic Variable Elimination (SVE) to analytically solve the lower optimization. The resulting program can then be formulated as a mixed-integer linear program (MILP) which is solved to global optimality using standard off-the-shelf solvers. To our knowledge, our framework is the first to provide a globally optimal solution to the linear SPO problem. Experimental results comparing with state-of-the-art local SPO solvers show that the globally optimal solution obtains up to two orders of magnitude reduction in decision regret. Paper Code
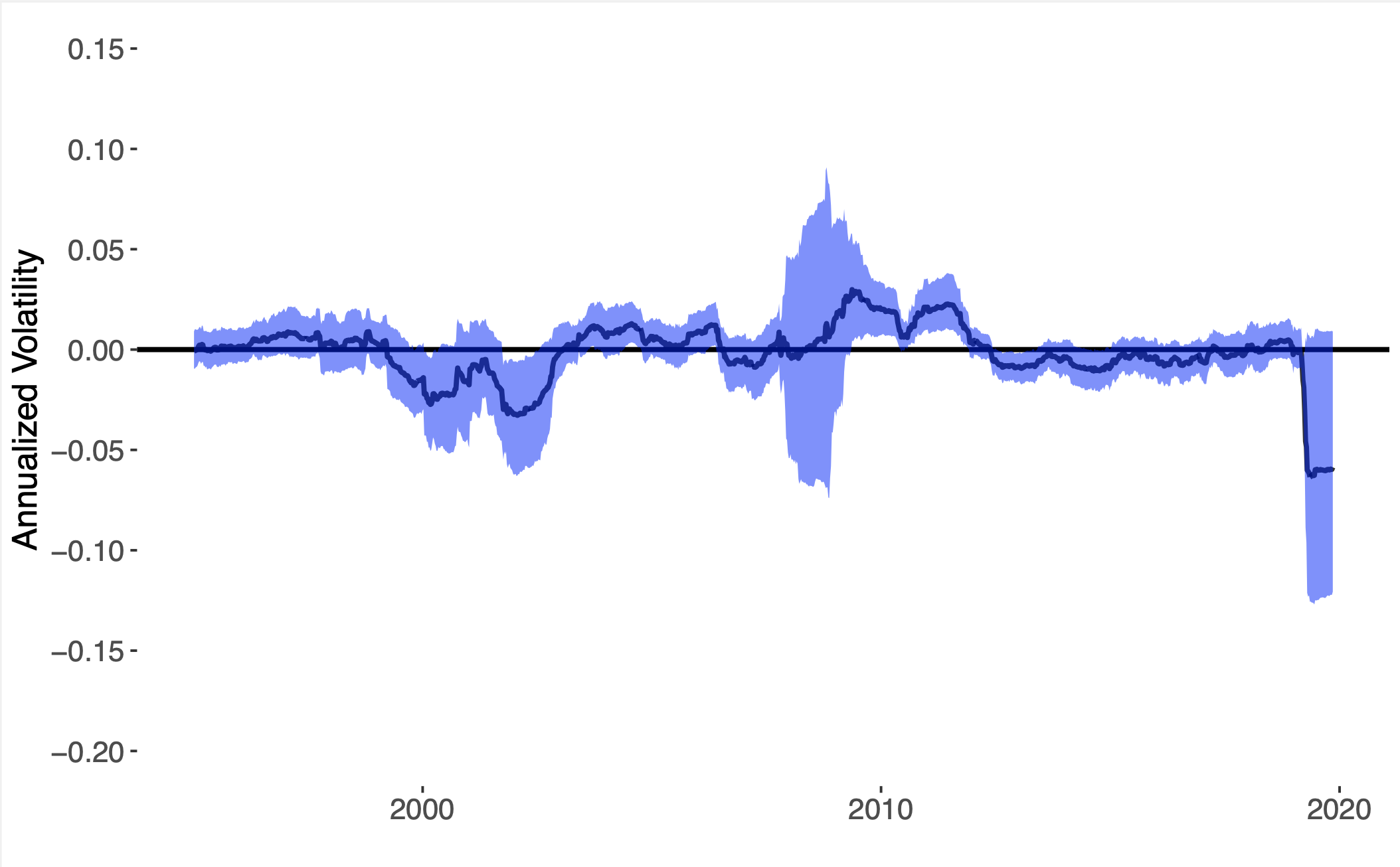
Integrated covariance estimation
| Volatility difference | Bootstrap variance |
|---|
 |  |
Paper
A Butler, RH Kwon. Covariance estimation for risk-based portfolio optimization: an integrated approach. Journal of Risk. 24 (2) 2021. Abstract
Many problems in quantitative finance involve both predictive forecasting and decision-based optimization. Traditionally, covariance forecasting models are optimized with unique prediction-based objectives and constraints, and users are therefore unaware of how these predictions would ultimately be used in the context of the models’ final decision-based optimization. We present a stochastic optimization framework for integrating time-varying factor covariance models in a risk-based portfolio optimization setting. We make use of recent advances in neural-network architecture for efficient optimization of batch convex programs. We consider three risk-based portfolio optimizations: minimum variance, maximum diversification and equal risk contribution, and we provide a first-order method for performing the integrated optimization. We present several historical simulations using US industry and stock data, and we demonstrate the benefits of the integrated approach in comparison with the decoupled alternative. Paper Code
RPTH: A differentiable risk-parity optimization library
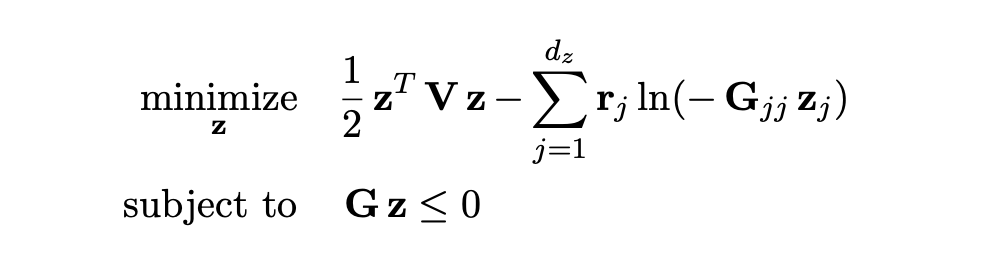
Description
RPTH is differentiable risk-parity optimization library implemented in PyTorch. Code
Efficient optimization in GP modelling
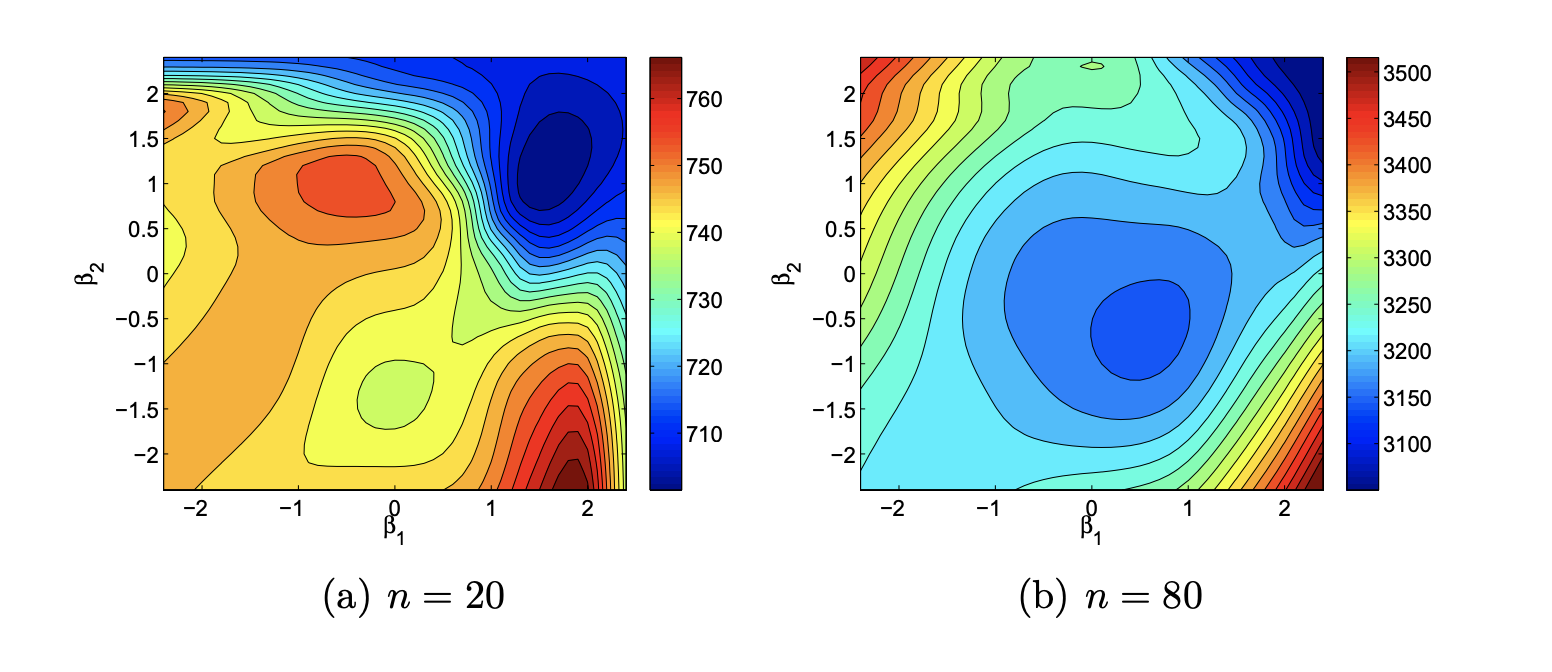
Paper
A Butler, RD Haynes, TD Humphries, P Ranjan. Efficient optimization of the likelihood function in Gaussian process modelling. Computational Statistics & Data Analysis. 2014. Abstract
Gaussian Process (GP) models are popular statistical surrogates used for emulating computationally expensive computer simulators. The quality of a GP model fit can be assessed by a goodness of fit measure based on optimized likelihood. Finding the global maximum of the likelihood function for a GP model is typically challenging, as the likelihood surface often has multiple local optima, and an explicit expression for the gradient of the likelihood function may not be available. Previous methods for optimizing the likelihood function have proven to be robust and accurate, though relatively inefficient. Several likelihood optimization techniques are proposed, including two modified multi-start local search techniques, that are equally as reliable, and significantly more efficient than existing methods. A hybridization of the global search algorithm Dividing Rectangles (DIRECT) with the local optimization algorithm BFGS provides a comparable GP model quality for a fraction of the computational cost, and is the preferred optimization technique when computational resources are limited. Several test functions and an application motivated by oil reservoir development are used to test and compare the performance of the proposed methods with the implementation provided in the R library GPfit. The proposed method is implemented in a Matlab package, GPMfit. Paper Preprint
Data-driven integration of regularized MVO portfolios
| Training loss | Realized Volatility |
|---|
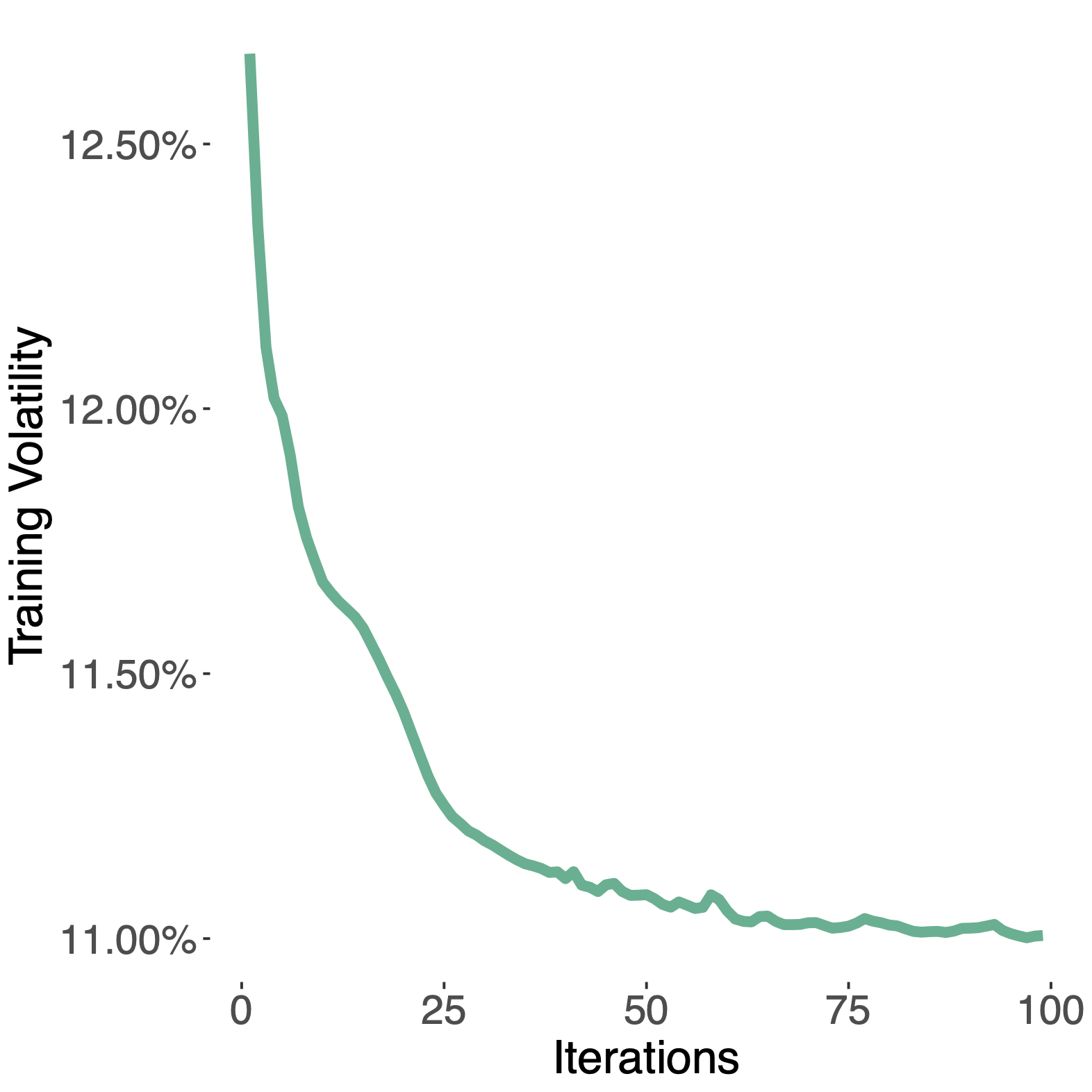 | 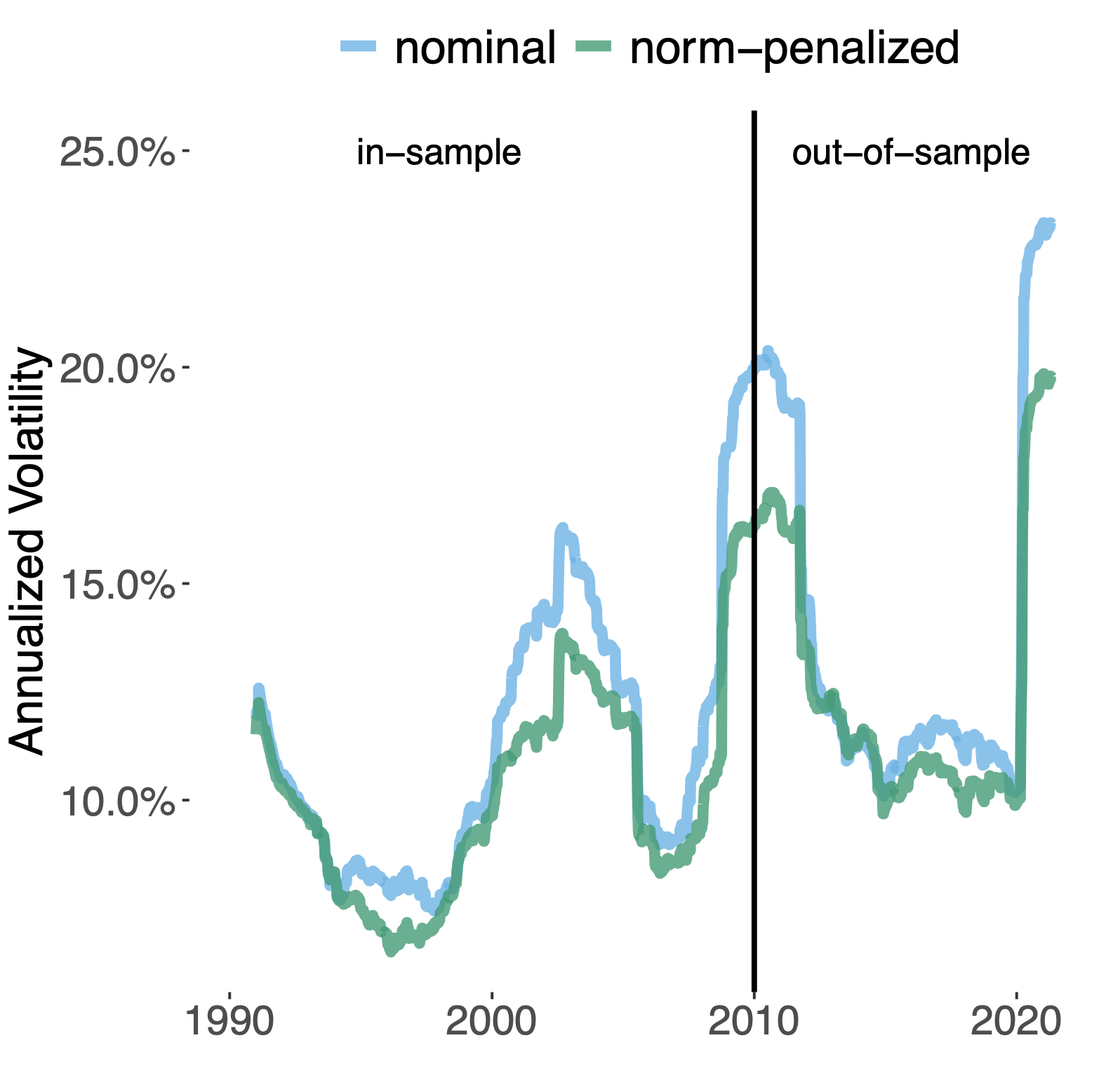 |
Paper
A Butler, RH Kwon. Data-driven integration of regularized mean-variance portfolios. 2021. (preprint) Abstract
Mean-variance optimization (MVO) is known to be sensitive to estimation error in its inputs. Norm penalization of MVO programs is a regularization technique that can mitigate the adverse effects of estimation error. We augment the standard MVO program with a convex combination of parameterized L1 and L2-norm penalty functions. The resulting program is a parameterized quadratic program (QP) whose dual is a box-constrained QP. We make use of recent advances in neural network architecture for differentiable QPs and present a data-driven framework for optimizing parameterized norm-penalties to minimize the downstream MVO objective. We present a novel technique for computing the derivative of the optimal primal solution with respect to the parameterized L1-norm penalty by implicit differentiation of the dual program. The primal solution is then recovered from the optimal dual variables. Historical simulations using US stocks and global futures data demonstrate the benefit of the data-driven optimization approach. Preprint